2.1. Gràfics vectorials

Els gràfics vectorials, també coneguts com gràfics orientats a objectes, són el segon gran grup d'imatges digitals. Són més simples que els gràfics de mapa de bits, ja que en ells les imatges s'enmagatzemen i representen per medi de traçats geomètrics controlats per càlculs i fórmules matemàtiques, agafant alguns punts de la imatge com a referència per construir la resta.

Per tant, les imatges vectorials no es dibuixen pixel a pixel, sino que es formen a partir de vectors, objectes formats per una sèrie de punts i línies rectes o corbes definides matemàticament.

Per exemple, una linia es defineix en un mapa de bits mitjançant les propietats de cada un dels pixels que la formen, mentre que un grafic vectorial es dibuixa per la posició del seu punt inicial i final, i una funció que descriu el camí entre ells.
Un cercle es defineix vectorialment per la posició del seu punt central (x,y) i pel seu radi.

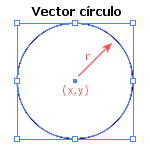
Cada vector en un gràfic vectorial té linia de contorn, amb un color i una amplada determinats, i pot estar farcit d'un color o ser transparent. Les caracteristiques del traç de contorn es poden canviar en qualsevol moment.

Les imatges vectorials s'emmagatzemen com una llista que descriu cada un dels seus vectors components, la seva posició i propietats.

En el cas de la resolució, els gràfics vectorials són independents de la resolució, ja que no depenen d'una retícula de pixels donada. Per tant tenen la màxima resolució que permet el format en el qual s'enmagatzema.

· Exemple de imatge vectorial enmagatzemada en un arxiu SWF (flash) incrustada en un document HTML:

La introducció d'objectes vectorials com el flash a les pàgines web va suposar un avenç considerable, ja que permeten incloure gràfics de tamany modificable sense pèrdua de qualitat, molt útils en logotips, plans, diagrames, etc.
Com a exemple, si es fa click a la imatge superior amb el botó dret del ratolí i se selecciona "Aumentar" (Zoom In) o "Reducir" (Zoom Out), aquesta cambiará de tamany conservant les seves caracteristiques visuals.

2.2. Objectes vectorials

Un objete vectorial és un element gràfico que té una forma definida amb un traçat. La forma d'un traçat de vectors es determina pels punts que atravessa. El color del traç dels objectes vectorials segueix el seu traç i el seu farcit (relleno) ocupa l'àrea interior del traç. El traçat i el farcit determinen l'aspecte de l'objecte quan s'imprimeix o es publica al Web.

Qualsevol eina de creació d'objectes vectorials (Illustrator, Freehand, Flash, Fireworks, o d'altres no comercials) disposen d'eines bàsiques que permeten dibuixar amb rapidesa linies rectes, cercles i elipses, quadrats i rectangles, estrelles y polígons equilàters.

Es poden dibuixar traçats de vectors d'estil lliure amb eines de traçat de vectors (com la línia) i amb la Pluma, que permet dibuixar formes complexes amb curves suaus i linies rectes punt a punt.

Eines principals d'una aplicació vectorial.

2.2.3. Corbes de Bézier

Els principals elements que constitueixen un vector són les corves de Bézier, desenvolupades per Pierre Bézier per encàrrec de Renault, que buscava una familia de corbes respresentables matemàticament (corbes de tercer grau) que permetessin representar les corbes suaus que desitjaven donar als seus automòbils.

Una corba Bézier queda totalment definida per cuatro punts caracteristics, els punts inicial i final de la corba (nodes o punts d'ancla) i dos punts de control, invisibles en el gràfic final, que defineixen la seva forma. Per modificar la seva forma, és suficient amb cambiar de posició un dels seus nodes o un dels seus punts de control.

Són corbes de control poc complexes i amb un dibuix suau, capaçes d'adaptar-se a gairebé qualsevol forma imaginable, per això es fan servir per dessenyar logotips i icones i per copiar qualsevol figura.

També són molt versàtils, poguent adoptar desde corbatures molt suaus (quasi linies rectes), a corbatures molt fortes (complexes), passant per tots els valors intermitjos. Poden, fins i tot, canviar de còncaves a convexes al voltant d'un punt.

2.3. Atributs dels objectes

Un objecte vectorial pot tenir diversos d'atributs, entre d'altres:

Traçat: Un traç que envolta l'objecte, de gruix modificable, i de diversos estils (punts, guions,...)

Farcit: farcit sòlid o degradats de diversos tipus (lineal, radial, de dos colors o més,...) o bé transparent (sense farcit)

Sobreimpressió: Un objecte pot tenir un atribut de sobreimpressió, que farà que aquest objecte s'imprimeixi per sobre de l'objecte que hi té a sota, creant una mescla de colors.

Rebentat: El programa n'augmenta, al voltant de l'objecte, els punts que desitjem per evitar l'anomentat error de registre.

Objectes malla: Els objectes malla ens permeten crear una malla totalment modificable que servirà de base per aplicar-hi un degradat. Els colors d'aquest degradat els indiquem als diversos punts que té la malla.

2.4. Eines de suport

Les aplicacions vectorials disposen d'eines que ajuden a crear els objectes.
Es pot activar una quadricula en la que nosaltres decidim la separació entre linies divisories en mil·limetres, punts, polzades, píxels, etc.

Hi han també guies que permeten la colocació exacta dels elements del document. Les podem posar exactament al punt que desitjem, indicant les coordenades. Es poden moure, esborrar o bloquejar.

També podem alinear uns objectes respecte altres, moure'ls, o d'altres accions que ajuden a mantenir les posicions correctes dels elements.

Els objectes se solen ordenar per capes, el que permet que es treballi sobre uns elements mentre altres estàn amagats o bloquejats, o també podem modificar les propietats de les capes, com disminuir-hi la opacitat, o fer-les servir com plantilles per calcar imatges externes enllaçades al document.

2.5. Modificació d'objectes

Els objectes vectorials tenen el gran avantatge de poder ser modificats de diverses formes, ja que la seva constitució es matemàtica (operacions de vectors) que .
Podem modificar un objecte pels punts que formen el traçat, podem escalar, rotar,... i gràcies a tots aquests modificadors aconseguim objectes molt més complexos.

2.5.1. Operacions booleanes amb objectes

Les operacions booleanes (basades en l'Àlgebra de Boole) permeten unir objectes, intersecar-los, retallar-los, només seleccionant els dos objectes destinats a la modificació i després triar una forma de combinació, retallat, o el que es desitji.

Pathfinder (Buscatrazos) d'Illustrator.

Amb aquest mètode es poden arribar a fer formes complexes que no es poden crear amb una eina bàsica d'un programa de creació de vectors. Algus exemples: